Hallo semuaa para pengunjung blog, yang hanya mau mampir atau
mau nyari pelajaran yang akan saya jelaskan, atau yang tiba-tiba nyasar ke blog
saya :v. selamat datang !
Nah, pada kesempatan kali ini saya akan menjelaskan satu
materi lagi yang masih berhubungan dengan matriks juga, yakni “Basis dan
Dimensi”. Langsung ajaa…
Sebelumnya kalian harus tahu nih, ada beberapa subbab yang
terdapat disini, kita akan membahasnya satu per satu .
Basis dan
Dimensi
· Ruang-n Euclides
Jika
n sebuah bilangan bulat positif, maka n-pasangan bilangan berurut
adalah sebuah urutan n bilangan real (x1,x2,…,xn).
Himpunan semua n-pasangan bilangan berurut dinamakan ruang-n
Eucides dan dinyatakan dengan Rn.
Definisi.
Misalkan u=[u1,u2,…,un];
v=[v1,v 2,…,vn]
vektor di Rn.
o u = v jika
hanya jika u1 = v1, u2
= v2,…, un = vn
o u + v
= [u1 + v1, u2
+ v2,…, un + vn
]
o ku =
[ku1, ku2,…, kun]
o u•v = u1v1
+ u2v2 + … + unvn
o |u| = (u•u)1/2
= 
·
Ruang Vektor
Misalkan
V sembarang himpunan. V dikatakan sebagai ruang vektor, apabila syarat-syarat
berikut dipenuhi :
1) Jika u
dan v vektor-vektor di V, maka u + v juga berada di V.
2) u+v = v+u
3) u+(v+w) = (u+v)+w
4) Ada sebuah vektor 0 di V sehingga 0+u=u+0
5) Untuk setiap u di V terdapat –u di V sehingga u+(-u)
= -u+u =0
6) Jika k skalar dan u di V, maka ku
berada di V
7) k(u+v) = ku + kv
8) (k + l)u = ku + lu
9) k(lu) = (kl)u
10)
1u = u
Langkah-langkah pengerjaan :
1. Tulis yang
diketahui
2. Buat
permisalan metriks A dan B dimana bentuknya seperti soal (S)
3. Jumlahkan
matriks A dan B
4. Cek, apakah
ketika dijumlahkan hasilnya merupakan elemen S
Jika
iya, maka syarat ke-3 terpenuhi
5. Lalu, ambil
salah satu matriks, kamudian kalikan denga konstanta (K)
6. Cek, jika
dikalikan hasilnya merupakan elemen S, maka syarat ke-4 terpenuhi
Catatan :
apabila salah satu syarat tidak terpenuhi, maka ia bukan sub ruang/ ruang
vektor.
·
Kombinasi Linier
Sebuah
vektor x dikatakan kombinasi linier dari vektor-vektor u1,
u2,…, un jika vektor tersebut dapat
dinyatakan dalam bentuk :
x = k1u1+ k2u2 +… + knun
dimana
k1, k2,…,kn adalah
skalar.
Langkah-langkah
unuk mengerjakannya ialah :
1. Tulis yang
diketahui
2. Subtitusikan
nilai-nilai yang diketahui ke rumus kombinasi linier
3. Ubah bentuk
vektor menjadi persamaan linier
4. Ada 2 opsi
yaitu, mengerjakan dengan elementasi subtitusi atau dengan metode Operasi Bris
Elementer
5. Kembalikan
lagi ke benuk persamaan linier (jika memakai OBE), lalu selesaikan persamaan
hingga mendapat nilai dari masing-masing k .
contoh
:
misal,
, u = [2,-1,3]T, v =
[1,2,-2]T, apakah x
= [8,1,5]T kombinasi
linier dari u dan v.
Jawab
Perhatikan
kombinasi linier x = k1u+k2v
[8,1,5]T = k1[2,-1,3]T + k2[1,2,-2] T
x = 3u
+ 2v
Dari
kesamaan vektor diperoleh :
Di
inverskan menjadi :
·
Membangun Ruang Vektor
Jika
u1, u2,…,un adalah
vektor-vektor pda ruang vektor V, dan jika setiap vektor x pada V dapat
dinyatakan sebagai kombinasi linier u1, u2,…,un,
maka u1, u2,…,un
dikatakan membangun ruang vektor V
Apabila
hasil determinan tidak sama dengan 0,
maka ia membangun/merentang.
Apabila hasil
determinan sama dengan 0, maka ia tidak
membangun/merentang.
Langkah-langkah
kerjanya ialah sebagai berikut :
1. Tulis yang diketahui
2. Berilah
perandaian/permisalan pada vektor x, karena pada soal spanning vector x tidak
di beri tahu
3. Subtitusikan
nilai-nilai yang diketahui ke rumus kombinasi linier
4. Ubah bentuk vektor ke
bentuk persamaan linier
5. Dari persamaan linier,
ubah ke bentuk matriks
6. Cari determinannya
(jika matriks berordo 3x3 bisa menggunakan metode sarrus, apabila lebih dari
3x3, bisa menggunakan metode ekspansi laplace, chio, Doolitle, crout)
7. Buat kesimpulannya.
Contoh:
Apakah, u=[1,2,-1]T, v=[-2,3,3]T, w=[1,1,2]T membangun R3?
Pembahasan :
Apabila x=[x1,x2,x3]T vektor di R3. Bentuk kombinasi linier,
x = k1u + k2v
+ k3w
[x1,x2,x3]T = k1[1,2,-1]T + k2[-2,3,3]T + k3[1,1,2]T
Dari kesamaan vektor
diatas, menghasilkan sistem persamaan linier sebagai berikut :
(Menghitung determinan
menggunakan metode sarrus)
·
Kebebasan Linier
Apabila
S = {u1, u2,…,un} adalah himpunan
vektor, S dikatakan bebas linier bilamana kombinasi linier :
k1u1
+ k2u2 + … + knun = 0
penyelesaiannya
adalah trivial yakni k1 = 0, k2 = 0,…, kn
= 0. Jika ada penyelesaian lain (non trivial), maka S dikatakan tak bebas
linier.
Contoh
:
Himpunan
vektor, S = {u1,u2,u3}, u1=[2,-1,3]T, u2=[1,2,-6]T, u3=[10,5,-15]T adalah vektor tak bebas linier, karena 3u1 + 4u2 = u3.
Apabila
hasil determinan tidak sama dengan 0,
maka ia (S) bebas linier.
Apabila
hasil determinan sama dengan 0, maka ia
(S) bukan bebas linier.
langkah-langkah mengerjakannya ialah :
1.
Tulis yang diketahui
2.
Subtitusikan nila-nilai yang diketahui
ke rumus kebebasan linier
3.
Ubah bentuk vektor ke bentuk bentuk
persamaan linier
4.
Persamaan linier ubah ke bentuk
matriks
5.
Hitung determinannya (jika matriks berordo
3x3 bisa menggunakan metode sarrus, apabila lebih dari 3x3, bisa menggunakan
metode ekspansi laplace, chio, Doolitle, crout)
6.
Buatlah kesimpilan dari jawaban.
Contoh
:
Himpunan
vektor, S = {u1,u2,u3}, dimana u1=[1,-1,2]T, u2=[-2,3,1]T, u3=[2,1,3]T adalah vektor bebas linier, k1u1 + k2u2
+ k3u3 = 0, ekuivalen
Pembahasan :
(Menghitung determinan
menggunakan metode sarrus)
·
Ruang Hasil Kali Dalam
Sebuah
hasil kali dalam (inner product) pada ruang vektor riil V adalah fungsi yang mengasosiasikan
bilangan riil [u,v] dengan masing-masing pasangan vektor u
dan v pada V sedemikian rupa sehingga aksioma-aksioma berikut ini :
§ [u,v] = [v,u] (aksioma
simetri)
§ [u+v,w] = [u,w]
+ [v,w] (aksioma penambahan)
§ [ku,v] = k[u,v] (aksioma
kehomogenan)
§ [u,u] ≥ 0 dan [u,u]
= 0 Û u=0 (aksioma kepositifan)
§ Contoh :
Jika u = [u1,u2,…,un],
dan v = [v1,v2,…,vn]
adalah vektor-vektor pada Rn, maka :
[u,v]
= u•v = u1v1 + u2v2
+ … + unvn
adalah hasil kali dalam pada ruang Euclides Rn.
Dan u dan v dikatakan ortogonal jika [u,v] = 0.
Jika u ortogonal terhadap setiap vektor pada V, maka u dikatakan
ortogonal terhadap V.
Basis Ortonormal
Sebuah himpunan vektor pada ruang hasil kali dalam dikatakan
ortogonal jika semua pasangan vektor-vektor yang berada dalam himpunan tersebut
ortogonal. Sebuah himpunan ortogonal yang setiap vektornya panjangnya 1 disebut
ortonormal.
Contoh :
S={u1,u2,u3} dengan u1=[1,2,1], u2=[1,-1,1],
dan u3=[1,0,-1]. Himpunan S adalah ortogonal pada R3,
karena [u1,u2]=[u1,u3]=[u2,u3]=0
§ Catatan :
Jika S = {u1, u2,…,un}
adalah adalah basis ortonormal untuk sebuah ruang hasil kali dalam V, dan jika x
sembarang vektor di V, maka :
x = [x,u1]u1 + [x,u2]u2
+ … + [x,un]un
§ Misalkan V ruang hasil
kali dalam dan {u1,u2,…,un}
himpunan ortonormal Jika W ruang yang dibangun oleh u1,u2,…,un
maka setiap vektor x dalam V dapat dinyatakan dengan : x = v
+ w dimana :
v = [v,u1]u1 + [v,u2]u2
+ … + [v,un]un
·
Perubahan Basis
Misalkan S={u1,u2,…,un}
basis lama ruang vektor V, dan B={v1,v2,…,vn}
basis baru untuk ruang vektor V. Misalkan pula [x]S
matrik koordinat x relatif terhadap S dan [x]B
matrik koordinat x relatif terhadap basis B. Hubungan antara [x]S
dan [x]B diberikan oleh persamaan :
[x]S = P[x]B dan atau [x]B=P-1{x]S
P adalah matrik transisi dari basis baru
B ke basis lama S, dimana kolom-kolom P adalah matrik-matrik koordinat dari
vektor-vektor basis baru relatif terhadap basis lama, yaitu :
P= |[v1]S [v2]S….[vn]S|
·
Basis untuk Ruang
kosong / Nilitas
Langkah-langkah
kerjanya ialah :
1. Hitung dengan
menggunakan metode OBE untuk mendapatkan matriks U.
2. Ubah matrik U menjadi
bentuk persamaan linier
3. Cari nilai x1,
x2, x3,…. (jika da yang bisa dimisalkan, boleh
dimisalkan)
4. Hitung vektor dari Sistem
Persamaan Linierberdasarkan x1, x2, x3,….xn
Catatan :
o Vektor baris = vektor yang terletak pada baris
o Vektor kolom = vektor yang terletak pada
kolom
Terima
kasih! telah membaca sampai bawah, kurang lebihnya saya sebagai penulis blog
memohon maaf. Dan apabila ada kritik, komentar, dan saran atas kesalahan dan
kekurangan, bisa langsung tulis saja pada kolom komentar yang sudah tersedia.
Semoga bermanfaat :)




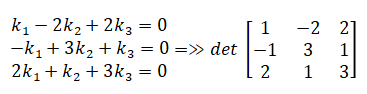



Tidak ada komentar:
Posting Komentar