Hallo semuaa para pengunjung blog, yang hanya mau mampir atau
mau nyari pelajaran yang akan saya jelaskan, atau yang tiba-tiba nyasar ke blog
saya :v. selamat datang !
Nah, pada kesempatan kali ini saya akan menjelaskan satu
materi lagi yang masih berhubungan dengan matriks juga, yakni “Diagonalisasi”.
Langsung ajaa…
Diagonalisasi
Matrik bujur sangkar A dikatakan dapat didiagonalisasi jika
terdapat matrik P yang mempunyai invers sedemikian rupa sehingga, P–1AP
adalah matrik diagonal. Matrik P dikatakan mendiagonalisasi A.
Sedangkan cara untuk menentukan nilai eigen dan vektor eigen
adalah sebagai berikut :
4. Setelah itu, hitung
akar-akar persamaan karakteristik (nilai lamda)
6. Bantuklah matrik P = [p1
p2 … pn] dan hitunglah P–1
7. Hitung, D = P–1AP
dengan diagonal utama, l1, l2, … ,ln
Setelah tahu langkah-langkah pengerjaannya, mari kita lihat
contoh soal dan pembahasan berikut, kalo bisa sambil dicoba juga biar bisaa…
Contoh soal :
Pembahasan :
2. Hitung determinannya :
|
|
|
(Disini
saya menggunakan metode gauss)
6. Bantuklah matrik P = [p1
p2 … pn] dan hitunglah P–1
Hitunglah P–1
(Disini saya menggunakan metode Operasi Baris Elementer)
7.
Hitung, D = P–1AP dengan diagonal utama, l1, l2, … ,ln
Catatan
:
·
Untuk menghitung invers matriks berordo 2x2
·
Untuk menghitunga inves matriks berordo 3x3 keatas dapat
menggunakan metode adjoint, operasi baris elementer, perkalian elementer, dan
partisi matriks.
Nah, begitulah cara menghitung nilai eigen dan ektor eigen
dengan matriks berordo 2x2 dan 3x3 .
Terima
kasih! telah membaca sampai bawah, kurang lebihnya saya sebagai penulis blog
memohon maaf. Dan apabila ada kritik, komentar, dan saran atas kesalahan dan kekurangan,
bisa langsung tulis saja pada kolom komentar yang sudah tersedia. Semoga
bermaat.


















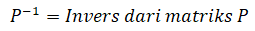




Tidak ada komentar:
Posting Komentar