Hallo semuaa para pengunjung blog, yang hanya mau mampir atau
mau nyari pelajaran yang akan saya jelaskan, atau yang tiba-tiba nyasar ke blog
saya :v. selamat datang !
Nah, pada kesempatan kali ini saya akan menjelaskan satu
materi lagi yang masih berhubungan dengan matriks juga, yakni “Mencari Nilai
Eigen dan Vektor Eigen”. Langsung ajaa…
Pasti kalian bertanya-tanya, apasih nilai eigen dan vektor
eigen itu?
Sebelumnya kita kenalan dulu yuk sama materinyaa…
Mencari
Nilai Eigen dan Vektor Eigen
Andaikan A marik bujur sangkar berordo nxn, vektor taknol x
di dalam Rn dikatakan vektor eigen A, jika tedapat skalar
taknol l sedemikian
rupa sehingga,
Ax = lx
l disebut
dengan nilai eigen dari A dan x disebut vektor eigen dari A yang bersesuaian
dengan l.
Contoh :
Vektor x = [1,2] adalah vektor eigen dari :
yang bersesuaian dengan nilai eigen, l = 3, karena :
Sedangkan cara untuk menentukan nilai eigen dan vektor eigen
adalah sebagai berikut :
4. Setelah itu, hitung
akar-akar persamaan karakteristik (nilai lamda)
Nah, setelah tahu langkah-langkah pengerjaannya, langsung saja
kita hitung sesuai langkahnya :
Selamat mencoba !
Contoh soal:
Pembahasan :
2. Hitung determinannya :
3. Hitung persamaan
karakteristiknya dan akar-akar persamaan karateristiknya (langkah no. 3 &
4) :
Nah, diatas adalah cara untuk menentukan nilai eigen dan vektor
eigen dari matriks berordo 2x2, adapun cara menghitung nilai eigen dan vektor
eigen dengan matriks berordo 3x3 dan selebihnya sama saja degan cara diatas,
namun yang perlu diperhatikan ialah saat menghitung determinannya (langkah 2)
yakni bisa menggunakan cara sarrus, ekspansi laplace, chio, crout, doolitle.
Seperti pada contoh berikut :
Contoh soal:
Pembahasan :
2. Hitung determinannya :
3. Hitung persamaan
karakteristiknya dan akar-akar persamaan karateristiknya (langkah no. 3 &
4) :
(menggunakan metode gauss)
Catatan : saat menghitung SPL
(menggunakan gauss) lebih baik diagonalnya diubah dulu ke angka satu dari kolom
perkolom, agar mempermudah saat menrubah ke angka 0.
Nah, begitulah cara menghitung nilai eigen dan ektor eigen
dengan matriks berordo 2x2 dan 3x3 .
Terima
kasih! telah membaca sampai bawah, kurang lebihnya saya sebagai penulis blog
memohon maaf. Dan apabila ada kritik, komentar, dan saran atas kesalahan dan
kekurangan, bisa langsung tulis saja pada kolom komentar yang sudah tersedia.
Semoga bermanfaat :)

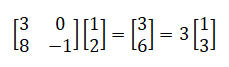








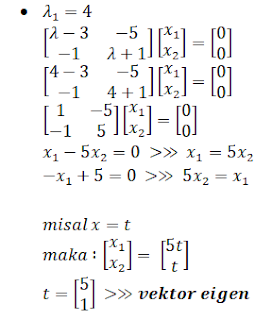













Tidak ada komentar:
Posting Komentar